设计原理
官方的白皮书已经比较详尽的描述了 v3 的设计原理,这里仅对白皮书中的内容做一些补充,包含本人对其中一些机制的理解和思考。
此图展示了一个 x⋅y=kx⋅y=k 的函数曲线图。为了满足让用户可以选择只在 [a,b][a,b] 价格区间内提供流动性。对于图中 [a,b][a,b] 区间的任意点,都有:
x=xvirtual+xrealy=yvirtual+yrealx=xvirtual+xrealy=yvirtual+yreal
其中 xreal,yrealxreal,yreal 分别表示用户提供的 x token, y token 数量,xvirtual,yvirtualxvirtual,yvirtual 分别表示流动池虚拟出的 x token y token 数量。当流动池的价格来到用户设置的零界点时(例如图中的 a 点或者 b 点),用户实际提供的 x token 或者 y token 将为 0,x 或 y 将完全由虚拟 token 组成。当价格进一步变动,移动到用户设定的价格区间之外时,流动池将移除这部分流动性,以保证虚拟的 x token 或 y token 数量不会减少,因此这部分虚拟的 token 只会在价格处于设定的区间内时参与价格的计算,而不会真的参与流动性提供。
例如,当价格到达 a 点时,用户的所有资金转换为 x,此时 yreal=0,y=yvirtualyreal=0,y=yvirtual,当价格继续降低时,流动池将移除这部分流动性。用户的资金状态将停留在 a 点,直至价格再次回到 a 点并进入 [a,b][a,b] 价格区间。
通过这样的设计,用户的资金只会在 [a,b][a,b]价格区间内提供流动性,并且因为虚拟 token xvirtual,yvirtualxvirtual,yvirtual 的参与,这部分流动性也满足 x⋅y=kx⋅y=k 公式,计算价格的方式并没有产生变化。
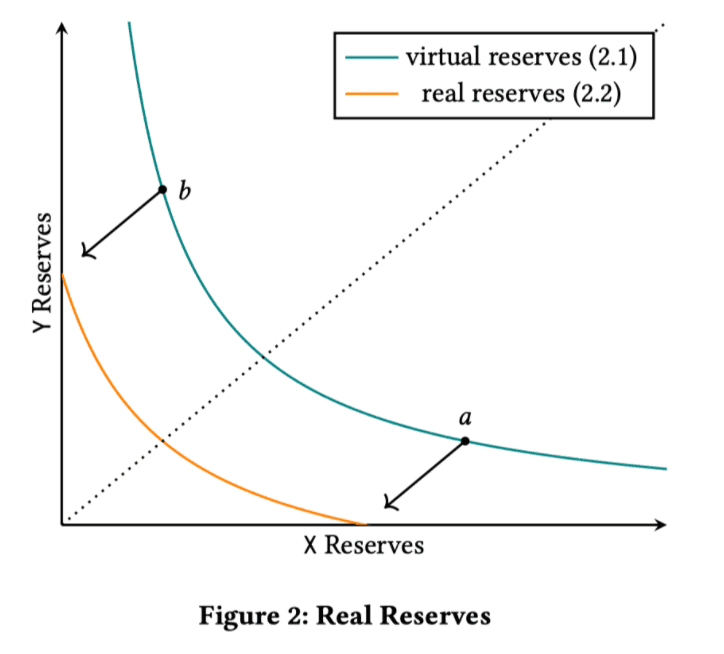
上图展示了用户选择在价格 [a,b][a,b] 之间提供流动性时,通过虚拟 token 的参与,将曲线 f(real)f(real) (橘红色)向右上方移动至 f(virtual)f(virtual)(绿色),实现了价格计算的一致性(即满足x⋅y=kx⋅y=k)。
交易过程
v2 版本
在 v2 版本中,用户与一个交易对发生交易时,假设用户提供 x token,资金量为 ΔxΔx,AMM 需要计算出用户可以得到的 y token,即 ΔyΔy. 如下图所示,池中资金从 a 点随着曲线移动到 b 点:
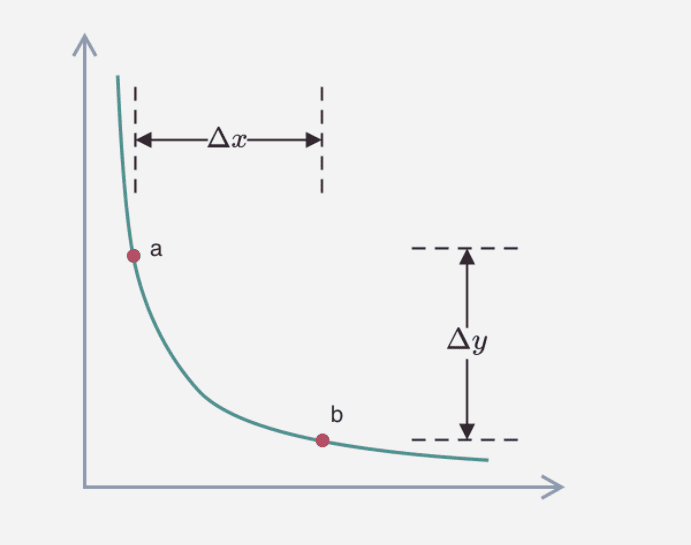
可以用过下面步骤计算 ΔyΔy:
x⋅y=(x+Δx)(y−Δy)=kx⋅y=(x+Δx)(y−Δy)=k
计算出:
Δy=y−x⋅yx+Δx=Δxyx+ΔxΔy=y−x⋅yx+Δx=Δxyx+Δx
具体的实现,可以参考 v2 代码实现。
v3 版本
在 v3 版本中,因为一个交易池中会有多个不同深度的流动池(每一个可以单独设置交易价格区间),因此一次交易的过程可能跨越多个不同的深度:
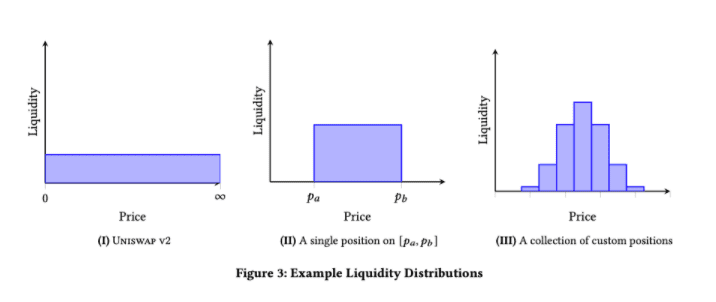
如上图最右边所示,当价格变化时,流动池中的总流动性也会随之变化。因此 v3 版本流动池中资金的关系不能像 v2 版本一样用一个平滑的 bonding curve 曲线来表示。那么如何计算交易结果呢?
因为 v3 版本交易可能并不在一个平滑的曲线中进行,需要根据池中资金的价格,选用不用的流动性来进行计算。流动性可以用 kk 表示,即 k=x⋅yk=x⋅y,用 PP 表示 xx 的价格,即 P=yxP=yx
因为每一次的价格变动都可能会引起流动性的变化,v3 需要围绕价格来进行交易相关的计算,例如当使用 x token 交换 y token 时:
交易至指定价格(通常是某一个流动性的价格边界)PP,需要的 x token 数 ΔxΔx,可以获得的 y token 数 ΔyΔy
给定 x token 数 ΔxΔx(假设此交易不会引起流动性发生变化),可以获得的 y token 数 ΔyΔy,以及最终的价格 PP
当 k 值不变时,根据定义:
{x⋅y=kP=yx{x⋅y=kP=yx
可以推导出:
⎧⎩⎨⎪⎪x=kP−−√y=kP−−−√⇒⎧⎩⎨Δx=Δ1P−−√⋅k−−√Δy=ΔP−−√⋅k−−√{x=kPy=kP⇒{Δx=Δ1P⋅kΔy=ΔP⋅k
这样一来计算过程并不需要关注池中的 x token 和 y token 余额,通过 kk 值和价格 PP 就可以完成交易过程的计算。
为了减少计算过程中的开根号运算,v3 合约直接存储 P−−√P 的值,同时合约中没有存储 kk 的值而是存储 L=k−−√L=k,通过 LL 来表示池中当前的流动性大小(存储 LL 还有一个好处是减少溢出的可能性)。
在实际交易过程中,一个交易可能跨越不同的流动性阶段,因此合约需要维护每个用户提供流动性的价格边界,当价格到达边界时,需要增加或移除对应流动性。通过分段计算的方式完成交易结果的计算,具体的实现过程会在后面的代码分析中讲解。
价格精度问题
因为用户可以在任意 [P0,P1][P0,P1] 价格区间内提供流动性,




